A few days ago I started working on auto calibration for shinytouch. Someone worked it a bit brfire and gave some PyGTK code that did fullscreen correctly but I ended up getting too confused (especially with embedding the video and images and threading delays). So now I started from scratch (or moreover continuing with using pygame) and now it is inherently not full screen. The auto calibration works by setting the contents of he window to be one color and taking a snapshot. After that the color is changes again and the snapshot is once again recorded. After gathering a pair, the software compares them pixel by pixel. It takes multiple trials and takes the average.

Then there is a function that makes cool stuff happen. It goes right to left to search for massive groups of consecutively marked hot pixel change areas. Ir searches for a general trapezoidal shape. And takes the lenghs and heights and positions. And right now, typing on my iPhone I wish the spell corrector was as awesome as the google wave contextual system. So in the near future, shinytouch will be as simple as launchingthe app and hitting a calibrate button and the computer does the rest. Maybe it might ask you to touch the screen in a special magic box or click on your finger afterwards but overall, zero setup and almost no calibration. So on another note, shinytouch is now almost a month old idea-wise. In my idea book, the references to it date back to June 28, though it may have originated a few days prior. For shinytouch the beginning window is quite a bit more broad. Anywhere from last year to march. I seem to recall late January experimentation with mirrors. So now, With shinytouch being the more promising (more acessible and radical) I have stalled development on mirrortouch. It’s quite annoying how fast time passes. There is so much that I really want to do but there is nost not enough time.

So I was looking through wikipedia to find out if there were some magical equations to govern how it should mix the color of the background screen contents and the reflection and make the application work better. I think Fresnel’s equations fit that description. It basically gives the reflectiveness of the substance from information about the substance, the surrounding substance (air) and the angle of incidence.

A really intimidating image from none other than Wikipedia

It’s quite interesting, partly because the shinyness (and thus the ratios used to combine the background color with the finger to compare) depends on the angle of the webcam to the finger, which depends on the distance (yay for trigonometry?). So the value used isn’t the 50-50 ration that it currently uses in the algorithm universally, but it’s dependent on variables to Fresnel’s Equations and the distance of the finger.

I forgot what this was supposed to describe

Anyway, time for a graphic that doesn’t really explain anything because I lost my train of thought while trying to understand how to use Inkscape!

So here’s something more descriptive. The two hands (at least it’s not 3, and why they’re just lines with no fingers isn’t my fault) and they’re positioned at different locations, one (hand 1) is close to the camera while the second (hand 2) is quite far away. Because of magic and trigonometry, the angle of the hand is greater when it’s further away. Also, this plugs into Fresnel’s Equations which mean the surface is shinier for where hand 2 is touching while it’s less shiny for hand 1. So the algorithm has to adjust for the variation (and if this works, then it might not need the complex region specific range values).

Yay For Trig!

So here it’s pretty ideal to have the angle be pretty extreme right? Those graphs sure seem imply that extreme angles are a good thing. But no, because quite interestingly, the more extreme the angle is, then the less accurate the measures from the x axis become. So in the image below, you can see that cam b is farther from the monitor (and thus has a greater angle from the monitor) and it can discern far more accurately depth than than cam a. The field of view for cam a is squished down to that very thin angle whereas the cam b viewing area is far larger. Imagine if there was a cam c which was mounted directly in front of the monitor, it would suffer from no compression of the x axis like a _or _b but instead it has full possible depth.

Extreme angles have lower precision

So for the math portion, interestingly, the plot for the decline in % of the total possible width is equivalent to the 1-sin() (I think, but if I’m wrong then it could be cos() and i suck at math anyway).

More Trig!

So if you graph out 1-sin(n) then you get a curve where it starts at 100% when the angle the camera is positioned at is 0 degrees from an imaginary line perpendicular to the center of the surface, and it approaches 0% as the degree measure reaches 90 deg.

So interestingly when you plot it, basically what happens is a trade-off between the angle the camera is at and the precision (% of ideal maximum horizontal resolution) and accuracy (shinyness of reflection). I had the same theory a few days ago, even before I discovered Fresnel’s Equations, though mine was more linear. I thought that it was just a point in which the values dropped for the shinyness. I thought that the reason the monitor was shinier from the side is that it was beyond the intended viewing angle, so since there is less light at the direction, the innate shinyness is more potent.

So what does this mean for the project? Well, it confirms my initial thoughts that this is far too complicated for me to do alone, and makes me quite sad (partly because of the post titled Fail that was published in january). It’s really far too complicated for me. Right now the algorithm I use is very approximate (and noticably so). The formula improperly adjusts for perception and so if you try to draw a straight line across the monitor, you end up with a curved section of a sinusoidal-wave.

Issues with algorithm

So it’s far more complicated than I could have imagined at first, and I imagined it as far too complicated for me to venture in this alone. But I’m trying even with this sub-ideal situation. So the rest of the algorithm for now will also remain with more linear approximations. I’m going to experiment in making more linear approximations of the plot of Fresnel’s equations. And hopefully it’ll work this time.

So Mirrortouch is really nice, it’s quite accurate, very fast, quite cheap and it’s my idea :)

But while trying to hook up the script to my webcam and looking at the live webcam feeds from it pointing at my monitor (aside from the awesome infinite-mirror effect!) I discovered an effect that’s quite painfully obvious but dismissed earlier: reflection.

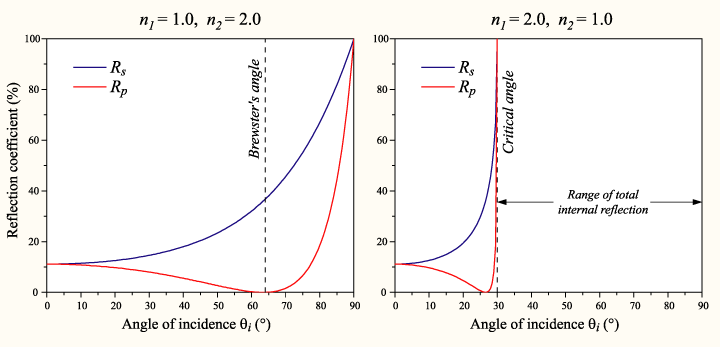
So a few months ago, I just sat in the dark with a few flashlights and a 6in square block of acrylic. I explored the multitouch technologies with them. Shining the flashlight through the side, I can replicate the FTIR (Frustrated Total Internal Reflection) effect used in almost all multitouch systems. Looking from under, with a sheet of paper over and shining the flashlight up, I can experiment with Rear DI (Diffused Illumination). Shining it from the side but above the surface, I can see the principle of LLP Laser Light Plane, actually here, it’s more accurately like LED-LP). MirrorTouch is from looking at it with one end tilted torward a mirror.

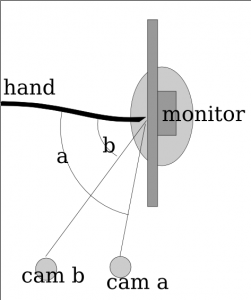
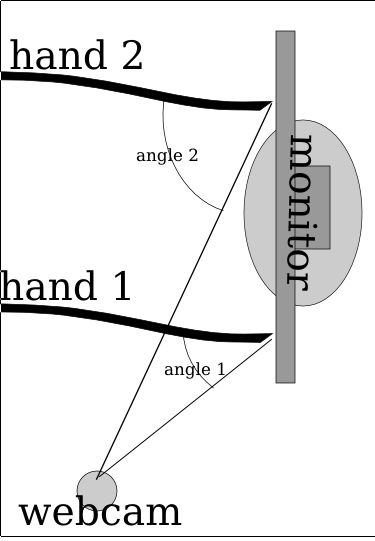
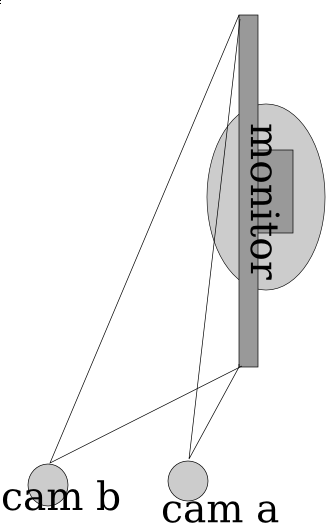
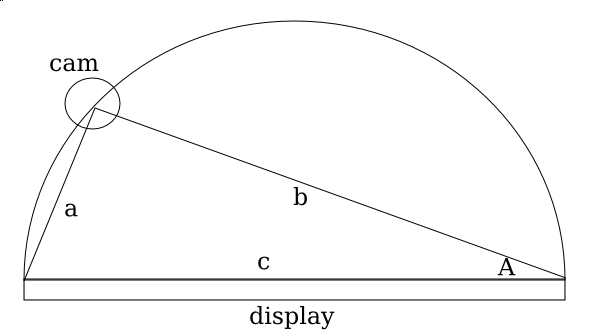
If you look at a mirror, and look at it not directly on, but at an angle, however slight, you can notice that the reflection (or shadow, or virtual image whatever you want to call it) only appears comes in “contact” with the real image (the finger) when the finger is in physical contact with the reflective medium. From the diagram below, you can see the essence of the effect. When there is a touch, the reflection is to the immediate right (in this camera positioning) of the finger. If the reflection is not to the immediate right, then it is not a touch.

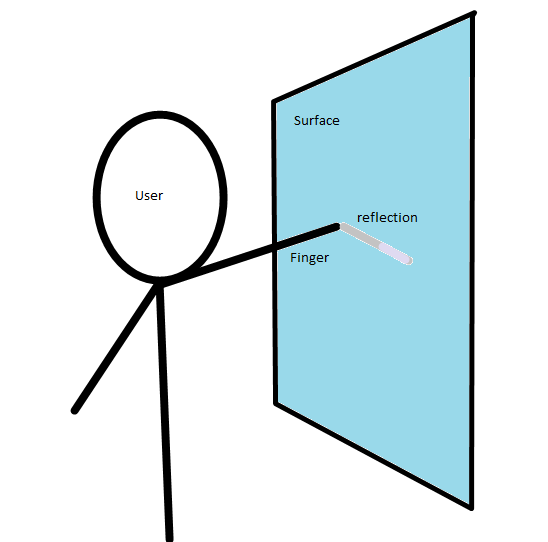
ShinyTouch Diagram

It’s a very very simple concept, but I disregarded it because real monitors aren’t that shiny. But when I hooked the webcam up to the monitor, it turns out it is. I have a matte display, and it’s actually really shiny from a moderately extreme angle.

So I hacked the MirrorTouch code quite a bit and I have something new: ShinyTouch (for the lack of a better name). ShinyTouch takes the dream of MirrorTouch one step further by reducing setup time to practically nothing. Other than the basic unmodified webcam, it takes absolutely nothing. No mirrors, no powered light sources, no lasers, speakers, batteries, bluetooth, wiimotes, microphones, acrylic, switches, silicon, colored tape, vellum, paper, tape, glue, soldering, LEDs, light bulbs, bandpass filters, none of that. Just mount your camera at whatever looks nice and run the software.

And for those who don’t really pay attention, this is more than finger tracking. A simple method of detecting the position of your fingers with no knowledge of the depth is not at all easy to use. The Wiimote method and the colored-tape methods are basically this.

The sheer simplicity of the hardware component is what really makes the design attractive. However, there is a cost. It’s not multitouch capable (actually it is, but the occlusion that it suffers from will deny the ability for any commonly used multitouch gestures). It’s slower than MirrorTouch. It doesn’t work very well in super bright environments and it needs calibration.

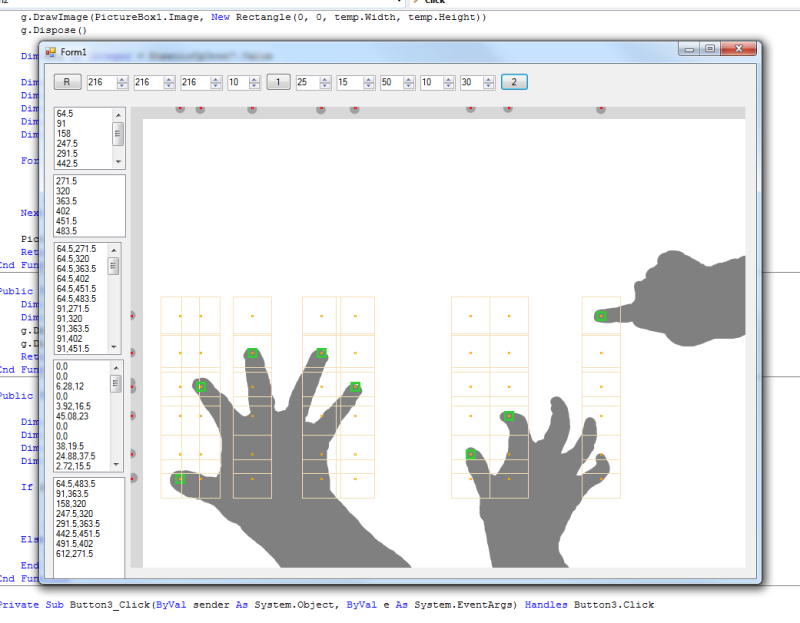
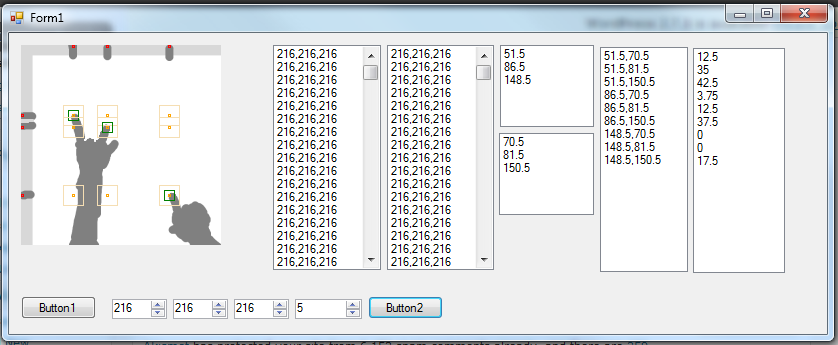
Calibration is at current stages of development, excruciatingly complicated. However, it can be simplified to be quite simple in comparison. The current one involves painful color value extraction manually from an image editor of your choice. Then it needs to run and you need to fix the color diff ranges. Before that you need to do a 4-click monitor calibration (which could theoretically be eliminated). But it could be reduced by making the camera detect a certain color pattern from the monitor to find out the corners and totally remove the 4 point clicking calibration. After that, the screen could ask you to click a certain box on the screen which would be captured pre-touch and post-touch and diff’d to get a finger RGB range. From that point, the user would be asked to follow a point as it moves around the the monitor to gather a color reflection diff range.

The current algorithm is quite awesome. It searches the grid pixel-by-pixel scanning horizontally from the right to the left (not left to right). Once it finds a row of 3 pixel matches for the finger color, it stops parsing and records the point and passes it over to the reflection analysis program. There are/were 3 ways to search for the reflection. The first one I made is a simple diff between the reflection and the surrounding. It finds the difference between the color of the point immediately to the right and the point to the top-right of the finger. The idea is that if there is no reflection, then the colors should basically roughly match and if it’s not then you can roughly determine that it is a touch.

This was later superseded by something that calculates the average of the color of the pixel on the top-right of the finger and the color of the finger. The average should theoretically equate the color of the reflection, so it diffs the averaged color with the color to the immediate right (the hypothetical reflection) and compares them.

There was another algorithm that is really simple for when it’s very very bright (near a window or something) and the reflection is totally overshadowed (pardon the pun, it wasn’t really intended) by the finger’s shadow. So instead of looking for a reflection, it looks for a shadow, which the agorithm thinks of as just a dark patch (color below a certain threshold). That one is obvoiusly the simples, and not really reliable either.

One big issue is that currently, the ranges are global, but in practice, the ranges need to vary for individual sections of the screen. So the next feature that should be implemented is dividing the context into several sections of the screen each with their own color ranges. It’s a bit more complex than the current system but totally feasable.

So the current program has the ability to function as a crude paint program and some sample images are on the bottom portion of this post.

purty2009-07-02T18:46:47.550169

purty2009-07-10T19:21:53.657122

purty2009-07-10T19:14:06.879415

purty2009-07-02T18:48:09.650197

Early on, I recognized one of the biggest issues with my idea for using mirrors was the computational power necessary to run the finger-position-detection algorithm. I recently thought, that that would be totally superfluous. My new idea is to use software to search a 1-pixel wide band of the mirrors to create several points. Those points are all combined to a list of all possible permutations. Each point goes through a method of determining whether or not it’s a fingertip. The easiest way, (and likely quite wildly inaccurate in the real world), is to measure the perimeter of a square that has that point of the center and compare it to the percent of that perimeter which is different from the surroundings. So then, you find the ones which work at all, and then you have your points!

I actually made a rough proof-of-concept system for this. It uses a very crude method of determining the different blobs on the mirrors (contiguous same color). And it uses a very crude surrounding box perimeter-ratio system. It’s to serve as a proof-of-concept type thing, not necessarily the precursor to an actual program that does something along the lines of it.

Fast Multitouch Image Processing

As for how fast it is, i’m not sure. I don’t even know how things like touchlib do it. If they scan through every pixel, and do more processing, then this is easily 50x faster. The speed of this is very largely dependent on the number of fingers touching it. w+h+4bf^2 would be a rough approximation of how many pixels would be needed to processed to get the result (w = width resolution, h = height resolution, b = size of surrounding box, f = number of fingers). On the Proof-of-concept, the input data is 200x200, The box set to a width of 20px, and there are 3 fingers touching, meaning ~1120 pixels searched. And if you were to scan through all the pixels (as I originally thought the idea would require), it would be wh, or 200*200, or 40,000. So the speed increase is by a factor of 36x, which is totally awesome. But again, I don’t know how others do it, they may have already an even faster way. But last year, I made a sort of object-tracking thing, which worked by scanning every pixel, and it was able to work at quite decent speed. So this, being an order of magnitude faster should work better.

Of course this is still a concept. There are still huge flaws not yet covered for like the fact in the real-world, the software would have to soemhow distinguish between the contents on the monitor and the hand in front. There may be a chance that someone is in an awkward position which tricks the software, the fact the software is completely useless on just about anything other than a fingertip, and many many more. I still find it interesting anyway :P