stuff by antimatter15

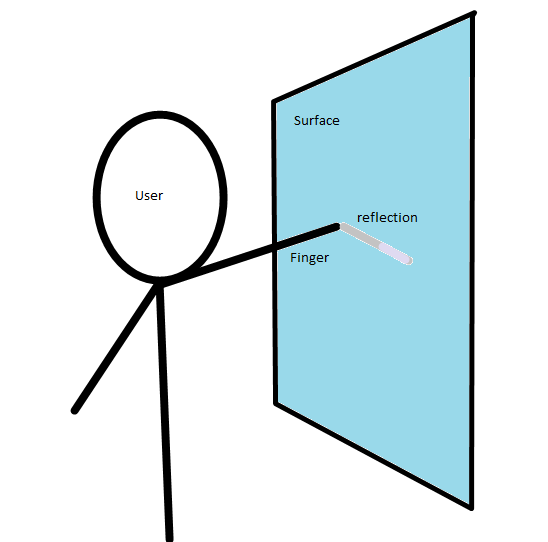
So I was looking through wikipedia to find out if there were some magical equations to govern how it should mix the color of the background screen contents and the reflection and make the application work better. I think Fresnel’s equations fit that description. It basically gives the reflectiveness of the substance from information about the substance, the surrounding substance (air) and the angle of incidence.

A really intimidating image from none other than Wikipedia

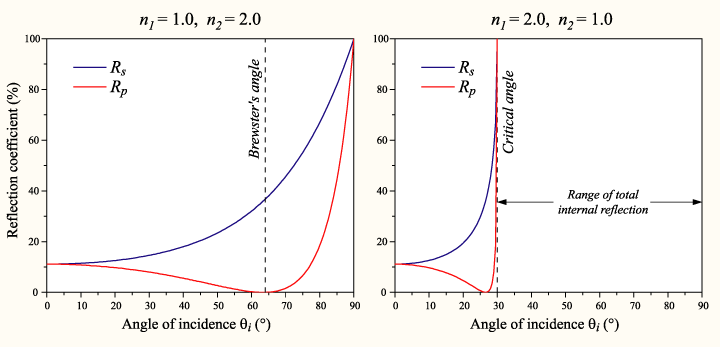
It’s quite interesting, partly because the shinyness (and thus the ratios used to combine the background color with the finger to compare) depends on the angle of the webcam to the finger, which depends on the distance (yay for trigonometry?). So the value used isn’t the 50-50 ration that it currently uses in the algorithm universally, but it’s dependent on variables to Fresnel’s Equations and the distance of the finger.

I forgot what this was supposed to describe

Anyway, time for a graphic that doesn’t really explain anything because I lost my train of thought while trying to understand how to use Inkscape!

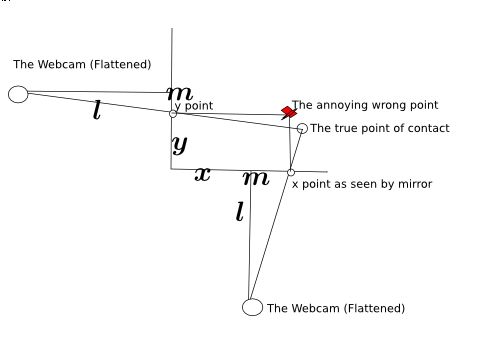
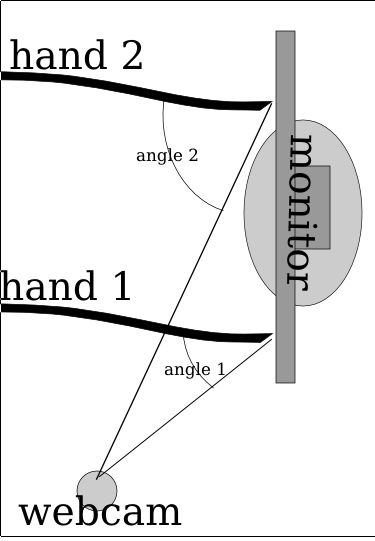
So here’s something more descriptive. The two hands (at least it’s not 3, and why they’re just lines with no fingers isn’t my fault) and they’re positioned at different locations, one (hand 1) is close to the camera while the second (hand 2) is quite far away. Because of magic and trigonometry, the angle of the hand is greater when it’s further away. Also, this plugs into Fresnel’s Equations which mean the surface is shinier for where hand 2 is touching while it’s less shiny for hand 1. So the algorithm has to adjust for the variation (and if this works, then it might not need the complex region specific range values).

Yay For Trig!

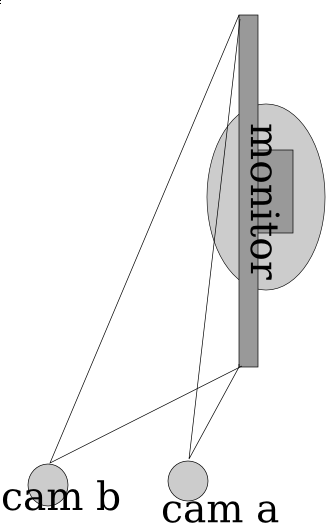
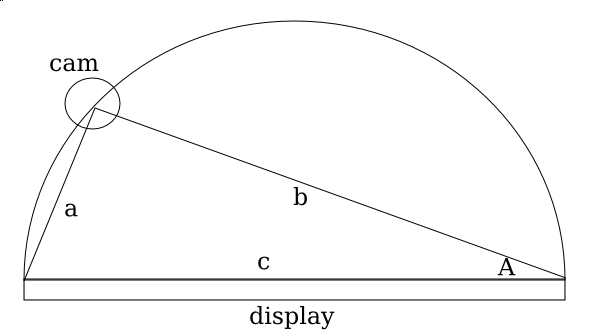
So here it’s pretty ideal to have the angle be pretty extreme right? Those graphs sure seem imply that extreme angles are a good thing. But no, because quite interestingly, the more extreme the angle is, then the less accurate the measures from the x axis become. So in the image below, you can see that cam b is farther from the monitor (and thus has a greater angle from the monitor) and it can discern far more accurately depth than than cam a. The field of view for cam a is squished down to that very thin angle whereas the cam b viewing area is far larger. Imagine if there was a cam c which was mounted directly in front of the monitor, it would suffer from no compression of the x axis like a _or _b but instead it has full possible depth.

Extreme angles have lower precision

So for the math portion, interestingly, the plot for the decline in % of the total possible width is equivalent to the 1-sin() (I think, but if I’m wrong then it could be cos() and i suck at math anyway).

More Trig!

So if you graph out 1-sin(n) then you get a curve where it starts at 100% when the angle the camera is positioned at is 0 degrees from an imaginary line perpendicular to the center of the surface, and it approaches 0% as the degree measure reaches 90 deg.

So interestingly when you plot it, basically what happens is a trade-off between the angle the camera is at and the precision (% of ideal maximum horizontal resolution) and accuracy (shinyness of reflection). I had the same theory a few days ago, even before I discovered Fresnel’s Equations, though mine was more linear. I thought that it was just a point in which the values dropped for the shinyness. I thought that the reason the monitor was shinier from the side is that it was beyond the intended viewing angle, so since there is less light at the direction, the innate shinyness is more potent.

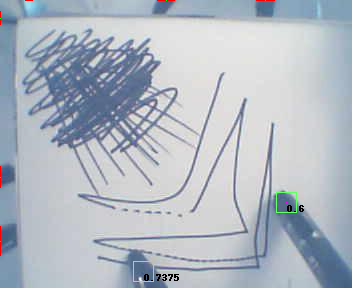
So what does this mean for the project? Well, it confirms my initial thoughts that this is far too complicated for me to do alone, and makes me quite sad (partly because of the post titled Fail that was published in january). It’s really far too complicated for me. Right now the algorithm I use is very approximate (and noticably so). The formula improperly adjusts for perception and so if you try to draw a straight line across the monitor, you end up with a curved section of a sinusoidal-wave.

Issues with algorithm

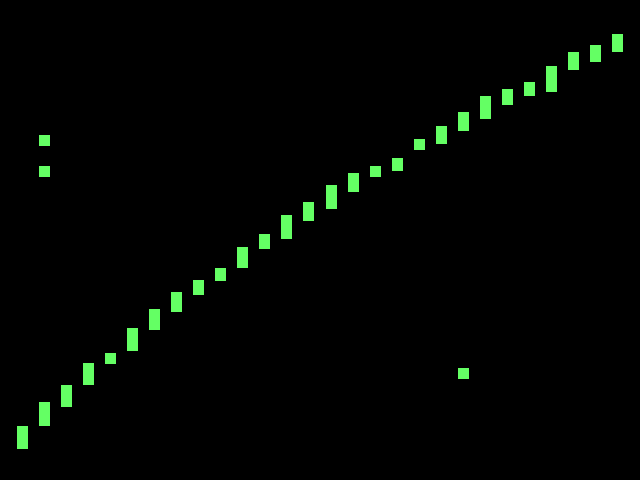
So it’s far more complicated than I could have imagined at first, and I imagined it as far too complicated for me to venture in this alone. But I’m trying even with this sub-ideal situation. So the rest of the algorithm for now will also remain with more linear approximations. I’m going to experiment in making more linear approximations of the plot of Fresnel’s equations. And hopefully it’ll work this time.

So Mirrortouch is really nice, it’s quite accurate, very fast, quite cheap and it’s my idea :)

But while trying to hook up the script to my webcam and looking at the live webcam feeds from it pointing at my monitor (aside from the awesome infinite-mirror effect!) I discovered an effect that’s quite painfully obvious but dismissed earlier: reflection.

So a few months ago, I just sat in the dark with a few flashlights and a 6in square block of acrylic. I explored the multitouch technologies with them. Shining the flashlight through the side, I can replicate the FTIR (Frustrated Total Internal Reflection) effect used in almost all multitouch systems. Looking from under, with a sheet of paper over and shining the flashlight up, I can experiment with Rear DI (Diffused Illumination). Shining it from the side but above the surface, I can see the principle of LLP Laser Light Plane, actually here, it’s more accurately like LED-LP). MirrorTouch is from looking at it with one end tilted torward a mirror.

If you look at a mirror, and look at it not directly on, but at an angle, however slight, you can notice that the reflection (or shadow, or virtual image whatever you want to call it) only appears comes in “contact” with the real image (the finger) when the finger is in physical contact with the reflective medium. From the diagram below, you can see the essence of the effect. When there is a touch, the reflection is to the immediate right (in this camera positioning) of the finger. If the reflection is not to the immediate right, then it is not a touch.

ShinyTouch Diagram

It’s a very very simple concept, but I disregarded it because real monitors aren’t that shiny. But when I hooked the webcam up to the monitor, it turns out it is. I have a matte display, and it’s actually really shiny from a moderately extreme angle.

So I hacked the MirrorTouch code quite a bit and I have something new: ShinyTouch (for the lack of a better name). ShinyTouch takes the dream of MirrorTouch one step further by reducing setup time to practically nothing. Other than the basic unmodified webcam, it takes absolutely nothing. No mirrors, no powered light sources, no lasers, speakers, batteries, bluetooth, wiimotes, microphones, acrylic, switches, silicon, colored tape, vellum, paper, tape, glue, soldering, LEDs, light bulbs, bandpass filters, none of that. Just mount your camera at whatever looks nice and run the software.

And for those who don’t really pay attention, this is more than finger tracking. A simple method of detecting the position of your fingers with no knowledge of the depth is not at all easy to use. The Wiimote method and the colored-tape methods are basically this.

The sheer simplicity of the hardware component is what really makes the design attractive. However, there is a cost. It’s not multitouch capable (actually it is, but the occlusion that it suffers from will deny the ability for any commonly used multitouch gestures). It’s slower than MirrorTouch. It doesn’t work very well in super bright environments and it needs calibration.

Calibration is at current stages of development, excruciatingly complicated. However, it can be simplified to be quite simple in comparison. The current one involves painful color value extraction manually from an image editor of your choice. Then it needs to run and you need to fix the color diff ranges. Before that you need to do a 4-click monitor calibration (which could theoretically be eliminated). But it could be reduced by making the camera detect a certain color pattern from the monitor to find out the corners and totally remove the 4 point clicking calibration. After that, the screen could ask you to click a certain box on the screen which would be captured pre-touch and post-touch and diff’d to get a finger RGB range. From that point, the user would be asked to follow a point as it moves around the the monitor to gather a color reflection diff range.

The current algorithm is quite awesome. It searches the grid pixel-by-pixel scanning horizontally from the right to the left (not left to right). Once it finds a row of 3 pixel matches for the finger color, it stops parsing and records the point and passes it over to the reflection analysis program. There are/were 3 ways to search for the reflection. The first one I made is a simple diff between the reflection and the surrounding. It finds the difference between the color of the point immediately to the right and the point to the top-right of the finger. The idea is that if there is no reflection, then the colors should basically roughly match and if it’s not then you can roughly determine that it is a touch.

This was later superseded by something that calculates the average of the color of the pixel on the top-right of the finger and the color of the finger. The average should theoretically equate the color of the reflection, so it diffs the averaged color with the color to the immediate right (the hypothetical reflection) and compares them.

There was another algorithm that is really simple for when it’s very very bright (near a window or something) and the reflection is totally overshadowed (pardon the pun, it wasn’t really intended) by the finger’s shadow. So instead of looking for a reflection, it looks for a shadow, which the agorithm thinks of as just a dark patch (color below a certain threshold). That one is obvoiusly the simples, and not really reliable either.

One big issue is that currently, the ranges are global, but in practice, the ranges need to vary for individual sections of the screen. So the next feature that should be implemented is dividing the context into several sections of the screen each with their own color ranges. It’s a bit more complex than the current system but totally feasable.

So the current program has the ability to function as a crude paint program and some sample images are on the bottom portion of this post.

purty2009-07-02T18:46:47.550169

purty2009-07-10T19:21:53.657122

purty2009-07-10T19:14:06.879415

purty2009-07-02T18:48:09.650197

MirrorTouch Diagram

MirrorTouch (the new name for my mirror-based multitouch system). For those who don’t remember, it is a project to create a retrofittable cheap new technology for touch detection. It can be made of mostly off-the-counter or even household items. The software has the potential to be VERY fast, many orders of magnitude faster than the current technology. It is less seceptable to occlusion than many other technologies.

It began well over 2 months ago. It started out with IDEALISTIC paint sketches and then a VB.NET application to parse it. Then it was ported to Python and could handle the same sketches. After discovering that in real life the positioning of the points varies due to some very strange and illogical factor, the project had a several-month hiatus.

The issue is clearly demonstrated here:

Oh Noes!

Last week, I considered the project a failure. I was playing around with a flashlight and tried looking into the strange behavior of the light. And something began to dawn on me. The shape as on diagram 1, can be flattened out as a visualization for what it behaves like. So from the pyramid shape, it looks more like a little 4-pointed star. Since the mirror is only on two sides, you can simplify it to half a star emerging from a square.

Flattened Diagram

To the side is a geometicalified sketch of it from my notebook. Here you can see the relation between the point and where it shows up on the mirror.

From that, you can use the distance between m and the y point (y-m) and divide it all over the distance from the mirror to the webcam (l) and plug it into y=mx+c form. Repeat that over the x axis and you can use basic algebra to find the interesction.

From that is the new magical formula that powers the application:

Yay! Purtyful!

The new formula is so magical that it actually works. Yes, it’s amazing, it has survived the most strictest of tests of mathematical consistency. It works.…. At least in theory. Now what about scientific tests? Oh no! it actually has to work in the physical world? Oh no!

With these 2 magical equations. I have (theoretically) in an idealistic model of the system, solved the issue with distortion. It should theoretically resolve all issues with the system. It should work.

So i set up the model again, attaching my webcam to a ruler and taping it to a speaker. Taping mirrors down on a piece of paper, and this time, Scribbling down measurements on the side. I got it to work. Workign without resetting configuration every time it ran. It works. It truly actually works. Multi-Touch too.

Since I cant get the webcam to feed directly to the python script, I have to use Cheese (it’s a linux app for taking pics from a webcam) to save screenies of the webcam mounted percariously from a ruler using only a bit of transparent Scotch tape. I copy the images over to the mirrortouch directory and go in the commandline and type in python process.py and watch as lines of logging output fly past as the windows autoscrolls down filled with coordinates and color hashes.

I watch as it generates a .png file.

Yes it works! AMAZING!

Note: The random scribbles in the back aren’t for any contstructive purpose. No, actually they just stop my stupid webcam from adjusting the contrast and making everything all ugly and ewwie. If my webcam sucked less than maybe it would work but my webcam really does really really really suck.

Now if it could get ported over to somethign like C++, and actually parse a live video feed from the webcam then it may become an actual working implementable multitouch technology. As it stands, it’s just a multitouch proof of concept, and I don’t know C++ so it probably won’t work.

Anyone dying for the source code can find it in the SVN repository at : http://code.google.com/p/mirrortouch/ Just beware that it may take lots of scary and tedious configuring in current stages (Configuring color range of background in the band, configuring color range of target, setting distances and middle length and other horrors, but from the SVN you can also do the insanely boring act of running various images that are already there through the script, and most of the images just wont work even with replacing huge blocks of code).

So i had this little project involving a quote repository and due to some trouble installing the superior Chirpy system, I used RQMS and did a few changes to add features like ajax ranking so you don’t have to reload to rank something.

It only involved changing less than 10 lines and pasting a snippet of my vX Ajax library.

Replace lines 151, 152 and 153 with the following lines (respectively) in rash_output.php (the template).

<a href="?ratingplus<?=$GET_SEPARATOR_HTML?>id=<?=$row['id']?>" onclick="plus(<?=$row['id']?>);return false" class="quote_ratingplus">+</a>
(<span id="rating<?=$row['id']?>"><?=$row['rating']?></span>)
<a href="?ratingminus<?=$GET_SEPARATOR_HTML?>id=<?=$row['id']?>" onclick="minus(<?=$row['id']?>);return false" class="quote_ratingminus">-</a>

Then add the following somewhere arbitrary in the of rash_template.php

<script type="text/javascript">
var _=_?_:{}
_.ajax=_.X=function(u,f,d,x){x=window.ActiveXObject;x=new(x?x:XMLHttpRequest)('Microsoft.XMLHTTP');x.open(d?'POST':'GET',u,1);x.setRequestHeader('Content-type','application/x-www-form-urlencoded');x.onreadystatechange=function(){x.readyState>3&amp;&amp;f?f(x.responseText,x):0};x.send(d)}
_.id=_.G=function(e){return e.style?e:_.d.getElementById(e)}
_.d=document

function plus(ID){
    _.ajax("?ratingplus&amp;id="+ID, function(){
        _.G("rating"+ID).innerHTML = parseInt(_.G("rating"+ID).innerHTML)+1
    })
}
function minus(ID){
    _.ajax("?ratingminus&amp;id="+ID, function(){
        _.G("rating"+ID).innerHTML = parseInt(_.G("rating"+ID).innerHTML)-1
    })
}
</script>

I’ve packaged a sample rash template with the ajax functionality. You can get it here: http://drop.io/ajaxrash

And the purpose of this is of course for one of my new projects, BotBash a conversation repository between a little (really simple) bot i built and strangers on Omegle. You can see it in action on http://botbash.antimatter15.com

Though what I described earlier is totally capable of Multitouch, I think it would probably be better to use a somewhat simpler implementation that is single-touch only.